The Straggling Function. Energy Loss Distribution of Charged Particles in Silicon Layers

The statistical nature of the ionising process during the passage of a fast charge particle through matter results in large fluctuations in the energy loss (Δ) in absorbers, whose thickness is thin compared to the particle range.

The number of electron-hole pairs (J) is related to Δ by the expression J=Δ/P, where P is a proportional factor, which for silicon equals 3.68 eV. Both Δ and J are stochastic quantities. The probability functions f(Δ) and φ(J) are usually called energy loss distribution or straggling functions.

They can be described schematically by the position of the maximum of distribution function (Δp) and the full width at half maximum (w), with Δp being located at lower value compared to the mean energy loss obtained from Bethe-Bloch ‹Δ› (Fig.1).

(click here to download the C++ Bethe-Bloch calculator).

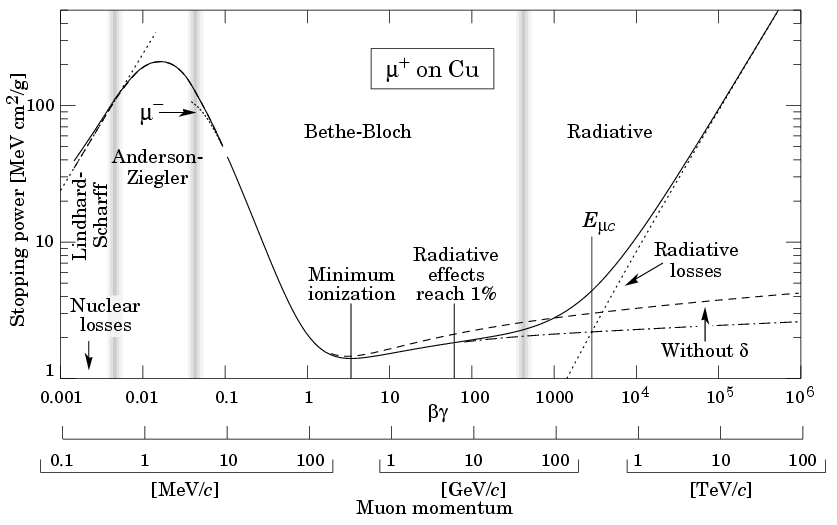
Fig.1 Stopping power for positive muons in cupper

Landau and Vavilov performed theoretical calculations on this distribution. Each of these solutions, however, has a different region of applicability and the distinguishing parameter in all these theories is the ratio k = ‹Δ› / E_max where E_max is the maximum transferable energy in a single collision.

Landau solved this problem for all situations where k ≤ 0.01, deriving the expected energy loss distribution by solving an integral transport equation:

distribution have been carried out by Landau and Vavilov

Here f(x,Δ) represents the distribution probability that the incident particle will lose an amount Δ of energy on traversing a layer of thickness x. W(E)dE denotes the probability per unit path length of a collision transferring energy E to an electron in the material.

The function W(E)dE is not generally known, but Landau was able to derive an approximate solution by using the free electron (Rutherford) cross section:

the free electron (Rutherford) cross section

with

keV μm-1 in silicon.

In the previous equation, z is the charge of the incident particle, Z and A are the atomic number and weight of the material, and ρ is the density. The Landau distribution is therefore given by [1]

with φ(λ) a universal function of the variable λ only

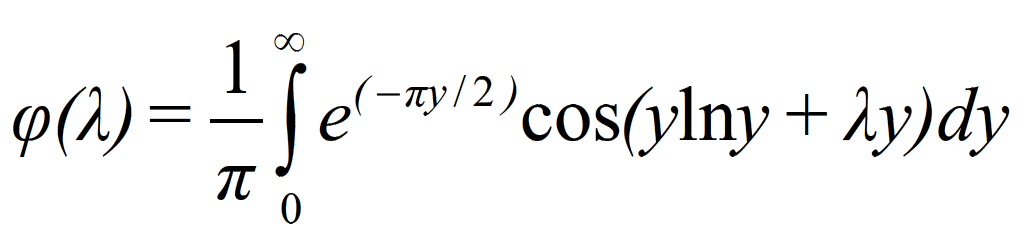
and

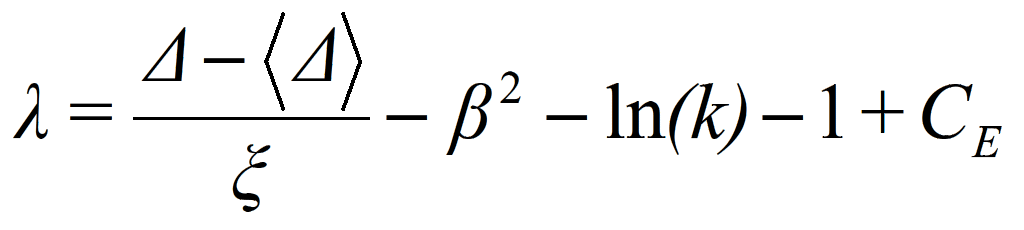
where C_E is the Euler constant equal to 0.5772. The Landau distribution, fL(Δ), is asymmetric with a tail extending to Emax with a maximum for λ=-0.229 and w=4.018ξ. This tail is mainly due to fast-emitted δ-rays. The energy loss corresponding to the maximum of the function fL(Δ) is the most probable energy loss [2]

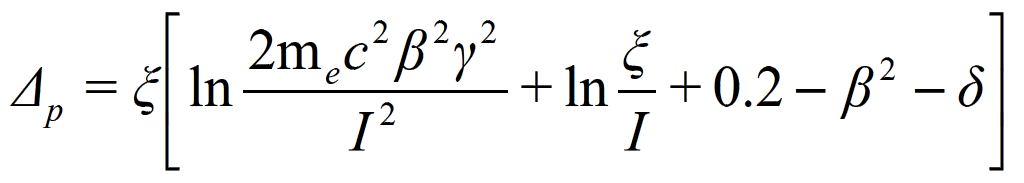
where I is the mean excitation potential and δ is the density correction. (click here to download the Matlab Landau Fit)

Fig.2 Stopping power for positive muons in cupper Straggling functions in silicon for 500MeV pions, normalized to unity at the most probable value Δp/x . The width w is the full width at half maximum.

Subsequently, Vavilov [3] derived an improved solution that takes into account the spin of the incident particle and introduces the physical limits coming from Emax. For the collision cross-section, Vavilov used the form

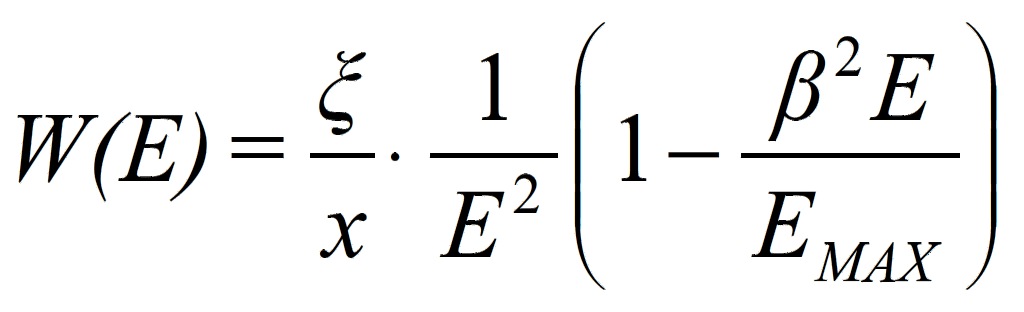
Interaction of Particles with Matter: From Theory to Measurements

Understand the Mysteries of Radiation: Master the Interaction with Matter in a Few Simple Steps

Get Your Copy Now

Vavilov also demonstrated that his solution tends to the Landau function for k ≤ 0.01, region where ‹Δ› is approximated to ξ. For instance, for 300 um silicon detectors, the convergence is already achieved by protons with momenta larger than 550 MeV/c. For k > 10, the number of collision is very large and, for the Central Limit Theorem, the Vavilov function coincides with Gaussian distribution, where the standard deviation is

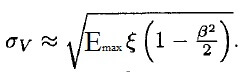
Fig. 3 Most probable energy loss in silicon, scaled to the mean loss of a minimum ionizing particle,388eV/μm (1.66 MeVcm2/g).

Landau-Vavilov solutions have been derived under the assumption that scatterings occur on quasi-free electrons. Therefore, they neglect the electron-binding energies. This assumption is a valid approximation only for close collisions.

Further corrections to the theory, taking into account the fact that the electrons in the material are not free, have been attempted by Blunck and Leisegang [4], Shulek [5] and Bichsel [6].

In the case of solid media, these calculations are aimed at the experimental observation that, while the most probable energy loss agrees rather well with the prediction of the theory, the width of the distribution is broader than expected and cannot be accounted for by electronic noise or imperfect resolution. The effect is particularly noticeable for very thin absorbers [7], of the order of a few hundred μm or less. The modified energy loss distribution can be improved by using a modified cross section to take into account the electron binding energy and the atomic shell structure. The modified energy straggling function can be expressed as:

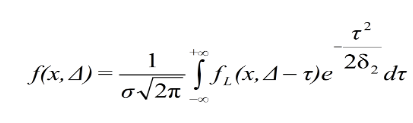
In other words, the experimentally observed energy spectrum can be calculated by convoluting the Landau distribution with a normal distribution of variance δ2. The result of the convolution is a broader distribution with a peak value that is usually increased by a small amount compared to the Landau theory. From the experimental observations, the δ2 value has been estimated:

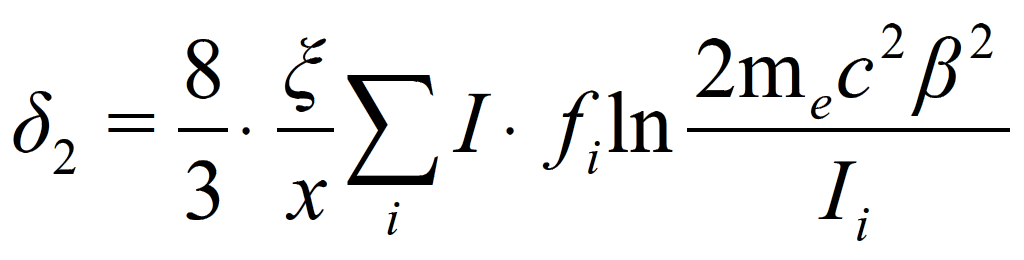
where f_i is the fraction of electrons in that shell. In silicon, this approaches a value of

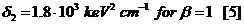
The resulting improved energy loss distribution has an overall value of w, which is roughly given by:

√[(4.018 ξ )^{^2} + ( 5.56 δ₂ )]

As the material thickness decreases, δ2 becomes more and more the dominant term, which determines the overall w of the straggling function. Conversely, it is not expected to provide an additional broadening of the distribution at large thicknesses.

As an example, in a 300 μm thick silicon detector, we get ξ is ~ 5.34 keV, √(δ₂) is ~ 5.76 keV, and an overall w is 25.4 keV (i.e., 18% larger than Landau width) for a relativistic β~ 1 and z = 1 particle in agreement with the experimental data.